プロセスシステム工学とかだとまああえてコンパートメントモデルとか言わないのだけど、主に臨床薬理の数値解析で出てくる感じだなあ。
なお、感染症でのコンパートメントモデルがあって、SEIRモデルとかある。
en.wikipedia.org
en.wikipedia.org
数値解析の話。
数値解析 - Wikipedia
まあ。
簡単にイメージを伝えると、例えば分子運動とかを数値解析する場合には、
- 分子間の力はだいたい原理的に基礎モデルはある。
- 分子が多くて代数的には解がない。
- じゃあ微小時間に区切って逐次加算していけばいいんじゃねえの?
というのを計算機などを使って力技でやるのが数値解析である。
収支の基本
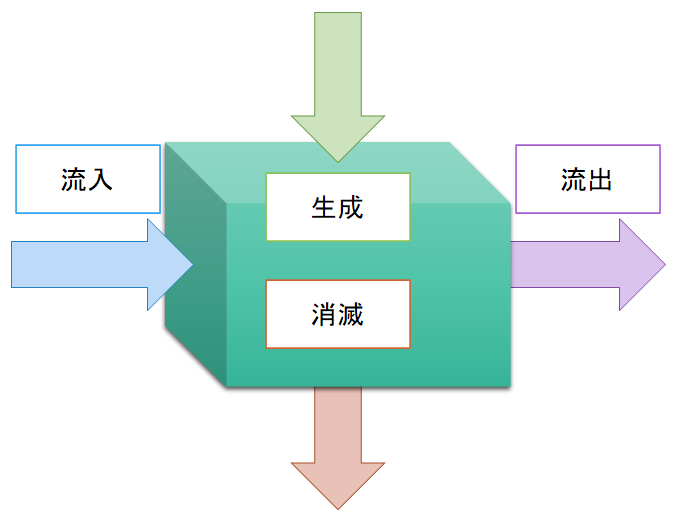
これらはプロセス工学では物質「収支」と言ったりするが、要は物質量不変の法則なんかをベースにして、微小時間でどのようになにかが増減するかを考える時に使う。
物質収支だと
- モノが系に入ってくる量
- モノが系から出ていく量
- モノが生まれる量(例えば化学反応で)
- モノが消失する量
この四パターンについて考えればいい。化学反応であれば、反応生成がモノが生まれる量になってくる。
それぞれを区切って考えるモデルが、コンパートメントモデルといえる。
SEIRモデルで考える際に考えられているコンパートメント
- Susceptible
- 未感染者
- Exposed
- 感染したが発症はしていない、伝染はさせない
- Infectious
- 発症者
- Recovered
- 回復し免疫を持った人
S→Eとなる速度、I→Eとなる速度、I→Rとなる速度それぞれあるが、そこはかなりゆるい条件で考えられている。
S→Eとなる速度は発症者の人数(全人口に対しての割合、簡単に言い換えると、例えば遭遇頻度とかになってくるか)に比例すると考えられている。濃厚接触しやすいしにくい等の細かい条件は考えられていない。I→E、I→Rは病気の種類によって速度が決まっている。
ついつい、「もっと正確なモデルを」と考えもするが、とは言え、これ以上複雑にしても情報が不足するので難しい。
現実から感染数を予想する事はもっと難しい。
見えている情報は遅延があり、また不完全である。特に感染したが発症していない人の数は読めない。現実の感染機会がのべーっとした理想的な感染の仕方を初期する訳もないので、結構その影響は無視出来ない。どうしたものかなあ。
一見すると当てはまりそうみたいなところを無理に当てはめても、見えない人がどれくらい読めるかは想定しづらい。